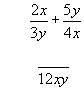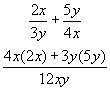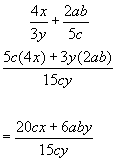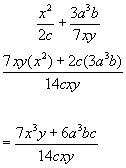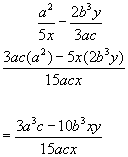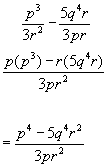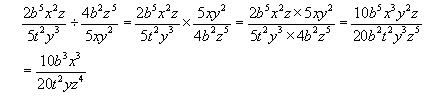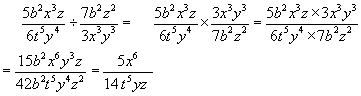Notes : Algebraic Expressions III

Assalamualaikum people,
There must be some of you that happens to be lost in my lecture session. Here I've already provide some notes that might helps you to understand.

Algebraic Fractions - Addition

This is just like number fraction addition, but with symbols.
To add two fractions you must first find their common denominator. Then convert each to the new denominator and add the new numerators.
The common denominator is found by multiplying the two numerators together.

In this case, multiply the 3y by the 4x. This gives12xy.
Now convert each factor to a factor of 12xy by dividing the denominator of each into 12xy and multiplying the result by each numerator(2x,5y)

Example #1

Example #2

Algebraic Fractions - Subtraction  

The method here is similar to addition, except the numerators(top terms) in the new fraction are subtracted.


Example #1

Example #2

Algebraic Fractions - Multiplication  

Simply multiply across the denominators and the numerators, keeping them separate. Cancel any terms where possible.

Example #1

Example #2

Algebraic Fractions - Division 

Simply invert the term you divide by(the 2nd term), and procede as for multiplication.

Example #1

Example #2

"Revisions help you to get a better result" - Teacher Ziha

Notes : Indices

Kindly click on the link below to download the recap about this topic.

Mind Map : Indices

 Indices

3³ ('3 cubed' or '3 to the power of 3') and 5² ('5 squared' or 5 'to the power' of 2) are example of numbers in index form.
3³ = 3×3×3
2¹ = 2
2² = 2×2
2³ = 2×2×2
etc.
The ² and ³ are known as indices. Indices are useful (for example they allow us to represent numbers in standard form) and have a number of properties.

 

Laws of Indices

There are several rules for dividing and multiplying numbers written in index form. These properties only hold, however, when the same number is being raised to a certain power. For example, we cannot easily work out what 2³×5² is, whereas we can simplify 3²×3³ .

 

Multiplication

When we multiply together index numbers, we add the powers. So:
y^a × y^b = y^a+b

 

Examples

x² × x³ = x⁵
5⁴ × 5^-2 = 5² (because 4 + (-2) = 2)
But there is no easy way of calculating 5⁴ × 3³ because 5 and 3 aren't the same number!

 

Division

When dividing index numbers, we subtract the power of the number we are dividing by from the power of the number being divided. So:
y^a ÷ y^b = y^{a - b}

 

Examples

x²/x³ = x^-1
7² ÷ 7^-5 = 7⁷

 

Brackets

(y^a)^b = y^a×b

 

Examples

(x²)³ = x⁶
(5³)² = 5⁶

Further Index Properties

Anything to the power 0 is equal to 1. So 3⁰ = 1, -824⁰ = 1 and x⁰ = 1.

 

Negative Indices

If you have a number raised to a negative power, this is equal to 1 divided by the number raised to the power made positive. In other words:
n^-a = 1/n^a.

 

Examples

n^-1 = 1/n.
3^-2 = 1/3² = 1/9
(½)^-3 = 2³ = 8

 

Fractional Indices

A fractional power means that you have to take a root of the number. For example, 4^½ means take the square root of 4 = 2. Similarly, x^1/3 means take the cube root of x.

We can use the rule (y^a)^b = y^a×b to simplify complicated index expressions.

 

Example

(1/8)^-1/3; = [(1/8)^-1]^1/3 = [8]^1/3 = 2

p/s: please write the index notation in the correct way. It might confuse you as well as ME.  

Untill then,

Thanks for reading this entry.

 Love, 

Cicer Ziha